Gauss's lemma
@needham2021visual page 274.
On a general surface, if we launch particles in all directions from a point $p$, travelling a distance $\sigma$ along geodesics, they will form a geodesic circle $K(\sigma)$ with radius $\sigma$ (this is a definition).
Lemma
The geodesic circle $K(\sigma)$ cuts its geodesic every geodesic radius at a right angle.
$\blacksquare$
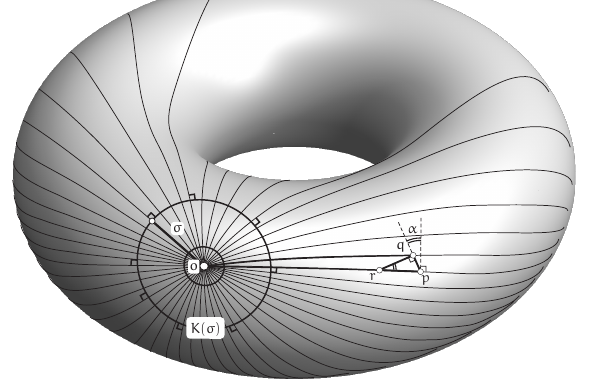
Proof
Idea: suppose $p$ is placed along a geodesic $\gamma_1$ from $o$ at distance $R$. Consider also the point $q$ at a nearby geodesic $\gamma_2$ to the previous one and at the same distance $R$. If the angle were lesser than $\pi/2$ we could look for a point $r$ on $\gamma_1$ such that we have a geodesic triangle $rpq$ with the angle at $q$ being $\pi/2$. In this case
$$ d(o,r)+d(r,q)By a symmetry argument (exchanging the roles of $p$ and $q$) it can be shown that the angle cannot be greater than $\pi/2$.
$\blacksquare$
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: